Free-Body Diagram
Table of Contents
Definition
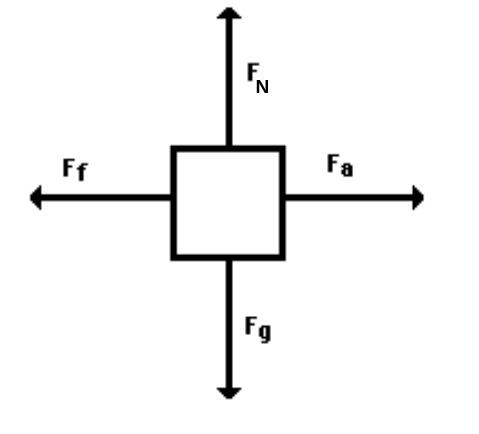
- pictures that show the size and direction of all forces acting on an object.
Steps to draw
- Pick one object to analyze
- Draw a box/point to represent the object
- Draw an arrow to represent each force acting on the object.
- Make sure the arrow shows the direction and relative size of the force.
Air Resistance
- a type of force.
- also known as air drag or aerodynamic drag, is a force that opposes the motion of an object through the air.
- think of it as friction but against gravity except it also works horizontally but its only for complex problems.
Formula: \(F_{air} = -kv^2\)
- \(k\) is a constant that depends on the object's shape and other factors.
- \(v\) is the object's velocity.
Vertical Equilibrium
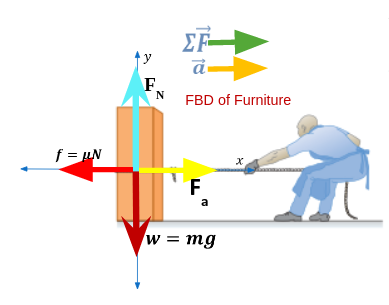
- It is the sum of vertical forces acting on the object.
- In static equilibrium, the sum of vertical forces is zero, meaning the normal force and weight balance each other.
- \(\sum\vec{F_y} = F_n - w = 0\) (for static equilibrium)
- \(\sum\vec{F}_y\) represents the sum of vertical forces.
- \(F_n\) is the normal force exerted by a supporting surface.
- \(w\) is the weight of the object due to gravity.
- \(\sum\vec{F}_y = N + P_y - w = 0\)
- More detailed version of the first formula.
- \(\sum\vec{F}_y\) represents the sum of vertical forces.
- \(N\) is the normal force exerted by a supporting surface.
- \(P_y\) is any vertical force component applied to the object.
- \(w\) is the weight of the object due to gravity.
Horizontal Equilibrium
- It is the sum of horizontal forces acting on the object.
- For horizontal equilibrium, the applied force and friction should balance each other out.
- \(\sum\vec{F_x} = F_a - f\)
- \(\sum\vec{F_x}\) represents the sum of horizontal forces.
- \(F_a\) is an applied force externally acting horizontally.
- \(f\) represents friction, which opposes motion.
- If pulling force \(F_a < friction\ f\) then furniture is at rest otherwise it will move to the right.
- \(\sum\vec{F}_x = P_x - f\)
- \(P_x\) is any horizontal force component applied to the object.
Net External Force
- The net external force acting on the object.
- The net external force determines the object's acceleration or state of rest. If it's zero, the object is in equilibrium.
- \(\sum\vec{F} = F_{ax} - f\) where \(\vec{F}\) is the net external force
- \(\sum\vec{F}\) represents the net external force.
- \(F_{ax}\) is the net applied force in the horizontal direction.
- \(f\) represents friction.
- \(\sum\vec{F} = P_x - f\)
- \(P_{x}\) is the net applied force in the horizontal direction.
- If \(\sum\vec{F}_y \neq 0\) then the object didn't touch the ground surface. Therefore, the net external force is \(\neq \sum\vec{F}_x\)
Static Friction
- Static friction is the friction force when two surfaces in contact do not move against each other, in other words it is the friction force at rest.
- if the applied force \(F_{a}\) exceeds the maximum static frictional force \(f_s\), then the object will finally move in the direction of the applied force.
- Scalar only.
- \(f_s = \mu_s\eta\)
- \(f_s\) - maximum static friction force
- \(\mu_s\) - coefficient of static friction
- \(\eta\) - symbol's name is eta magnitude of normal force.
- \(\mu \propto f\)
- \(f_s \propto F_n\)
Kinetic Friction
- Once an object is in motion, kinetic friction opposes the ongoing motion between the two surfaces.
- \(f_k = \mu_k\eta\)
- \(f_k\) - kinetic friction
- \(\mu_k\) - coefficient of kinetic friction
- \(\eta\) - symbol's name is eta is the normal force.
- always \(f_k < f_s\)