Analytical Method
Table of Contents
Definition
- The analytical method of adding vectors is divided into two: sine law and cosine law, and the component method.
Adding Two Vectors
Same Direction
- The magnitude of the resultant vector is given by the arithmetic sum of the magnitudes of the individual vectors. The direction follows that of the given vectors.
Given
\(\vec{A} = 20\ m/s,\ East\)
\(\vec{B} = 40\ m/s,\ East\)
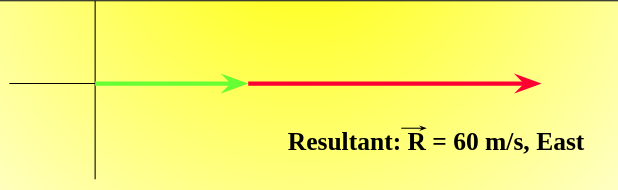\(20\ m/s,\ East + 40\ m/s,\ East \rightarrow \vec{R} = 60\ m/s East\)
Opposite Direction
- The magnitude of the resultant vector is given by the arithmetic difference of the magnitudes of the individual vectors. The direction follows that of the vector with bigger magnitude.
Given
\(\vec{A} = 15\ m,\ North\)
\(\vec{B} = 28\ m,\ South\)
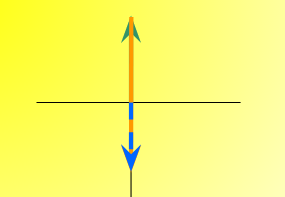\(15\ m/s,\ North + 28\ m/s,\ South \rightarrow \vec{R} = 13\ m\ South\)
Right Angle to each other
- You can use Pythagorean Theorem to find the resultant vector given the two vectors which are perpendicular.
Given
\(\vec{F}_1 = 6\ N,\ East\)
\(\vec{F}_2 = 5\ N,\ North\)
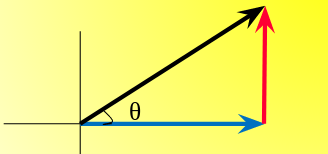
- Steps
- Use the pythagorean theorem to solve for the magnitude.
- To find the angle, use \(\displaystyle tan\theta = \frac{opp}{adj}\ or\ tan^{-1}\left(\frac{opp}{adj}\right)\)
- Answer: \(\vec{F}_R = 7.81 N, 39.81 ^{\circ} N of E\)
Cosine Law
- use it when you are given 2 sides and one angle in a triangle. Obviously, these triangles in this case is about vectors.
- Note: The range of \(cos^{-1}(x)\ |\ R = \{ 0, \pi \}\) so this is highly recommended to use instead of sine law.
Formulas:
\begin{align*} a^2 & = b^2 + c^2 - 2bc\ cosA \\ b^2 & = a^2 + c^2 - 2ac\ cosB \\ c^2 & = a^2 + b^2 - 2ab\ cosC \end{align*}Sine Law
- use it when you are given pretty much anything but be careful when given 3 sides and one angle.
- Note: The range of \(sin^{-1}(x)\ |\ R = \{ -\frac{\pi}{2}, \frac{\pi}{2} \}\) so
any angle larger than \(90^{\circ}\) or \(\frac{\pi}{2}\), we cannot use sine law for this.
- If you know that the angle is larger than \(90^{\circ}\), then subtract the result to \(180^{\circ}\).
Formulas:
\begin{equation*} \frac{a}{sinA} = \frac{b}{sinB} = \frac{c}{sinC} \end{equation*}Vector Resolution
- Vector Resolution. A single vector is usually divided into two vectors that are perpendicular to each other. These two vectors are called components and the process of splitting the vector into its components is called resolution.
- V is represented as \(V_x\) and \(V_y\) respectively.
- \(V_x = V cos\theta\)
- \(V_y = V sin\theta\)
- where θ is the angle that V makes with the x-axis.
Component Method
- It is generally used when more than two vectors are to be added.
- Steps
- Resolve the given vectors into its horizontal and vertical components.
Quadrant x y 1 + + 2 - + 3 - - 4 + - - Get the sum of the x-components and y-components which are also the x and y components for the resultant.
- Use the Pythagorean theorem to find the magnitude of the resultant vector. \(R^2=R_x^2 + R_y^2\)
- Use the signs of \(R_x\) and \(R_y\) to determine the quadrant.
Find the reference angle by taking the inverse tangent of the absolute value of the y-component divided by the x-component.
\begin{equation*} \theta = tan^{-1}|\frac{R_y}{R_x}| \end{equation*}